El aporte metodológico del factor Bayes más allá de las hipótesis de significación en la investigación clínica

The methodological contribution of the Bayes factor beyond the hypotheses of significance in clinical research.

Med Int Méx. 2021; 37 (3): 454-456. https://doi.org/10.24245/mim.v37i3.5172

Cristian Antony Ramos-Vera

Área de investigación, Facultad de Ciencias de la Salud, Universidad César Vallejo, Lima, Perú.

Señor Editor:

En el número 5 del volumen 36 de la presente revista se publicaron dos importantes artículos que reportaron asociaciones estadísticamente significativas (p < 0.05). El primer estudio estimó una correlación de mayor riesgo de la depresión en la calidad de vida en 94 adultos mayores mediante la prueba de razón de momios (odd ratios; OR).¹ La otra investigación evaluó una relación entre la existencia de síntomas gastrointestinales y la afectación hepática en 52 pacientes con diagnóstico de COVID-19 mediante la prueba de χ².² A su vez, este estudio reportó una diferencia significativa (t = -4.39) en las concentraciones de la transaminasa glutámico pirúvica (TGP; valor normal: 7-40 UI/L) entre los pacientes con (30) y sin (22) síntomas gastrointestinales.²

Se recomienda la replicación de las investigaciones clínicas basadas en las pruebas de significación para generar una evidencia con mayor credibilidad en el área de las ciencias de la salud.

El factor Bayes es el método idóneo para evaluar más allá de la interpretación dicotómica del rechazo o aceptación de la hipótesis nula, pues cuantifica el valor de evidencia o certeza en que los datos respaldan a la hipótesis alterna en relación con la hipótesis nula (hipótesis alterna vs hipótesis nula),^3,4 cuya utilidad es esencial para la inferencia estadística en las pruebas frecuentistas de estimación (por ejemplo, análisis de correlación o prueba estadística de comparación de medias de t de Student). Además, cuando se cuenta con hallazgos de significación, el modelo bayesiano es una alternativa metodológica de replicación estadística,^3,4 a partir del esquema de clasificación de Jeffreys:⁵ débil, moderado, fuerte, muy fuerte y extrema. Cuadro 1

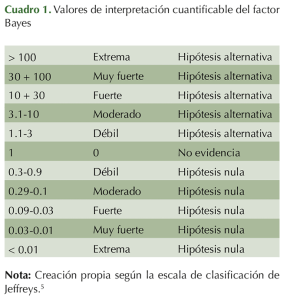
Esta carta tiene como objetivo reportar una serie de ejemplos de reanálisis bayesiano, con base en los valores estadísticos, las estimaciones de OR y χ² se convirtieron a coeficientes de correlación mediante una calculadora online;⁶ estos valores, junto al valor t del tercer hallazgo significativo y los datos muestrales respectivos, se consideran para la inferencia bayesiana.³

El factor Bayes consta de dos interpretaciones: FB₁₀ (a favor de la hipótesis alternativa) y FB₀₁ (a favor de la hipótesis nula) y el intervalo de credibilidad dado los datos, ante la evidencia de la hipótesis alterna (diferencia), este análisis se enfoca en el grado de certeza de esta hipótesis.

Los resultados, obtenidos mediante el factor Bayes son FB₁₀ = 227 y FB₀₁ = 0.004 e IC [0.201 a 0.544], con respecto al primer estudio (evidencia extrema). Así también se reportó: FB₁₀ = 8.415 y FB₀₁ = 0.119 e IC [0.121 a 0.585] para la relación entre los síntomas gastrointestinales y la afectación hepática (evidencia moderada), y FB₁₀ = 348 y FB₀₁ = 0.003 e IC [0.365 a 1.369] con respecto al hallazgo de diferencia significativa (evidencia extrema) del estudio de pacientes con COVID-19 de Pérez-Fernández y su grupo.²

La conversión del tamaño de efecto y otras medidas estadísticas que se basan en las hipótesis de significación (d, f, η2, OR, χ², Z) al efecto de correlación (r) de mayor uso universal en las ciencias de la salud permite afianzar futuros análisis y reanálisis bayesianos, estas estimaciones son fáciles de realizar mediante la calculadora de Lenhard y Lenhard.⁶ Asimismo, el factor Bayes es útil en otras pruebas estadísticas de significación,^7,8 cuyas medidas de tamaño de efecto también son convertibles.

El uso inclusivo de varias medidas estadísticas convertibles aumenta la inclusión de más investigaciones con diversos valores estadísticos de interés para futuros metanálisis. A su vez, la aplicación del factor Bayes es beneficiosa para seleccionar los resultados con mayor solidez de evidencia (FB₁₀ > 10) para el diseño del metanálisis, lo que afianza mayor credibilidad en las conclusiones de estas investigaciones sistemáticas.

Otro beneficio del factor Bayes es que permite detectar el mínimo tamaño muestral (FB₁₀ < 10) según el efecto mínimo de interés o el efecto clínicamente importante, que se selecciona con base en la evidencia de la bibliografía científica del tema de salud específico (por ejemplo, resultados metanalíticos previos de tamaño de efecto) con la finalidad de mejorar el diseño de futuros estudios, cuya mayor probabilidad bayesiana favorezca la obtención de resultados más concluyentes.

En conclusión, la inferencia bayesiana es esencial para precisar el grado de fuerza probatoria de las hipótesis estadísticas más allá del enfoque de las hipótesis de significación, y permite tomar decisiones clínicas importantes a partir de los resultados obtenidos de la salud de los pacientes en futuros estudios experimentales biomédicos y ensayos clínicos, entre otros.

REFERENCIAS

1. Viveros-García JC, Moreno-Cervantes CA, Yáñez-Quiñones DE, Luna-Torres S, et al. Efecto del control glucémico en la calidad de vida en ancianos mexicanos con diabetes. Med Int Méx 2020; 36 (5): 609-614. https://doi.org/10.24245/mim.v36i5.3152.
2. Pérez-Fernández GA, Isidor-Santana G, Martin-Rodríguez L. Síntomas gastrointestinales y afectación hepática en pacientes con el diagnóstico de COVID-19 en Santa Clara, Cuba. Med Int Méx 2020; 36 (5): 633-640. https://doi.org/10.24245/mim.v36i5.4370.
3. Ly A, Raj A, Etz A, Gronau QF, et al. Bayesian reanalyses from summary statistics: a guide for academic consumers. Adv Meth Pract Psychol Sci 2018; 1 (3):367-74. https://doi.org/10.1177/2515245918779348.
4. Marsmamn M, Wagenmakers EJ. Bayesian benefits with JASP. Eur J Dev Psychol 2017; 14 (5): 545-55. https://doi.org/10.1016/j.pmrj.2017.11.003.
5. Jeffreys H. Theory of probability. Oxford: Oxford University Press; 1961.
6. Lenhard W, Lenhard A. Calculation of effect sizes. Dettelbach: 2016. Disponible en: https://www.psychometrica.de/effect_size.html.
7. Kelter R. Bayesian alternatives to null hypothesis significance testing in biomedical research: a non-technical introduction to Bayesian inference with JASP: BMC Med Res Methodol 2020; 20: 1-12. https://doi.org/10.1186/s12874-020-00980-6.
8. Ramos-Vera CA. Replicación bayesiana: cuán probable es la hipótesis nula e hipótesis alterna. Educ Méd 2020. Epub 2020 Dic 02. https://doi.org/10.1016/j.edumed.2020.09.014.